Facebook Twitter Linkedin Copia Link

tag

protective shield with cyber security. Security and protection of personal data. The modern concept of mobile security.

Crittografia Post-Quantum: le sfide della transizione

Veronica Cristiano, Marco Rinaudo, Edoardo Signorini, Francesco Stocco

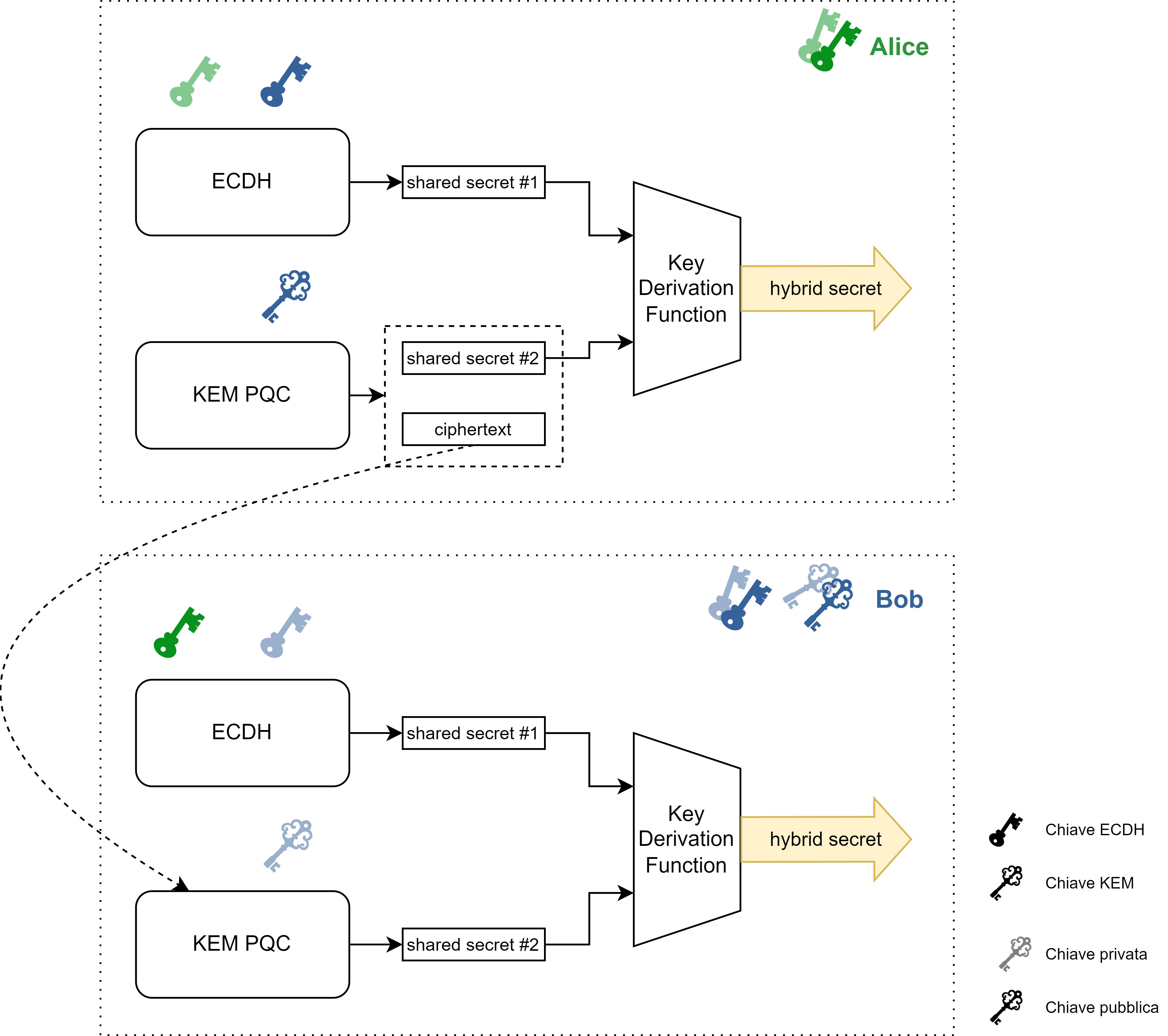
L’avvento del computer quantistico, seppur offra nuove opportunità, apre la possibilità ad attaccanti dotati di strumenti quantistici di sferrare attacchi agli attuali sistemi crittografici, con un impatto disastroso sulla sicurezza dei protocolli di comunicazione odierni. Per far fronte alla minaccia, la comunità scientifica internazionale si è mobilitata nella definizione di nuovi standard crittografici, resistenti a questo tipo di attacchi e implementabili su calcolatori classici. La transizione a schemi di crittografia post-quantum ha portato nuove sfide alle quali l’industria si sta preparando.

Scarica il PDF

Crittografia Post-Quantum...

3430 KB

Nei protocolli di comunicazione oggi utilizzati, tra cui il TLS (che protegge le comunicazioni Internet), la sicurezza dei dati è garantita da algoritmi crittografici afferenti a due principali famiglie:

chiave simmetrica: mittente e destinatario condividono una chiave segreta usata per cifrare e decifrare;
chiave pubblica: ogni utente ha una coppia di chiavi pubblica e privata. Chiunque può usare la chiave pubblica per cifrare, ma solo chi ha la chiave privata può decifrare.

In tali protocolli, gli schemi a chiave pubblica vengono usati per scambiare una chiave simmetrica con cui successivamente si cifrano i dati.

La minaccia del quantum computer

Nel corso degli anni ’80 [1] venne teorizzato un nuovo tipo di calcolatore, denominato quantum computer (QC), il cui funzionamento si basa su alcune leggi della meccanica quantistica. Tale oggetto, rimasto per molti anni un concetto puramente teorico, permetterebbe di risolvere alcune classi di problemi in modo estremamente più efficiente di quanto possibile con un computer classico. Tra i diversi campi in cui sono state indagate le potenzialità del QC vi è anche quello della crittoanalisi: nel 1994 l’americano Peter Shor descrisse un algoritmo in grado di risolvere in tempo polinomiale i problemi della fattorizzazione degli interi e del logaritmo discreto, su cui si basa la quasi totalità degli schemi a chiave pubblica attualmente utilizzati. Qualora venisse costruito un QC con sufficiente potenza per implementare l’algoritmo di Shor, diventerebbe quindi possibile rompere concretamente schemi quali RSA o ECDH, rendendo vulnerabili i dati scambiati attraverso il TLS o altri protocolli crittografici (es. VPN, app messaggistica).
Nel corso degli ultimi anni sono stati presentati i primi prototipi di QC che, pur non essendo ancora sufficienti per un utilizzo crittoanalitico, evidenziano importanti investimenti e il crescente rischio per la sicurezza delle informazioni. Inoltre, il futuro sviluppo di un QC può costituire un pericolo anche per i dati scambiati oggi: in un attacco “store now, decrypt later” l’attaccante intercetta i dati cifrati e li conserva fin quando non avrà un QC con cui recuperare i dati in chiaro. Tale attacco impatta soprattutto contesti che prevedono di mantenere cifrati i dati per lunghi periodi (es. dati sanitari o classificati) e rende necessario un avvio quanto più rapido della transizione verso soluzioni quantum resistant. Si rendono quindi necessari algoritmi a chiave pubblica non attaccabili da un QC, che formano la cosiddetta Post Quantum Cryptography o PQC.

La standardizzazione della PQC

Per fornire un riferimento univoco da seguire nell’implementare tali algoritmi, diversi enti di standardizzazione hanno intrapreso iter volti alla selezione dei migliori schemi PQC. Punto di riferimento è il processo indetto dal NIST americano: articolato su diversi round, svoltisi tra il 2016 e il 2022, ha portato alla pubblicazione di una bozza di standard per tre schemi PQC nell’agosto 2023. La versione definitiva è prevista entro fine 2024. Gli schemi presentati riguardano primitive di scambio chiave, tramite Key Encapsulation Mechanism (KEM), e di firma digitale. Mentre alcuni Paesi (ad es. Australia, UK, Canada) seguono quanto fatto dal NIST, altri governi hanno avviato processi indipendenti [2]. Tra questi possiamo ricordare:

Cina: avvio nel 2018 di un round di valutazione che ha portato, nel 2020, a selezionare tre schemi (diversi da quelli NIST);
Corea del Sud: nel 2021 ha inizio la competizione KpqC volta a standardizzare schemi PQC, non ancora conclusa.

In Europa, ANSSI (Francia) [3] e BSI (Germania) [4] hanno prodotto linee guida sulla PQC che prendono a riferimento la competizione NIST, ma se ne discostano in alcuni frangenti. In USA, la NSA ha aggiornato la suite di algoritmi CNSA per la protezione del segreto di stato includendo schemi PQC [5], definendo inoltre un piano di transizione (Fig.1).

Figura 1: Timeline per la transizione a CNSA 2.0

Clicca qui per ingrandire l'immagine

La matematica della PQC

La matematica è parte fondamentale della costruzione di schemi crittografici; infatti, la loro sicurezza si basa sulla difficoltà computazionale di risolvere un dato problema matematico. Se gli schemi di crittografia classica basano la loro sicurezza su problemi difficili per un calcolatore classico, il logaritmo discreto (ECDH) e il problema della fattorizzazione (RSA), gli schemi di crittografia post-quantum fondano la loro sicurezza su problemi diversi, difficili anche per un computer quantistico. La maggior parte di questi è costruita su oggetti matematici che danno il nome alle branche della PQC: lattice-based (reticoli), code-based (codici) e hash-based cryptography (funzioni di hash).

Reticoli
Un reticolo è definito, a partire da una base di vettori linearmente indipendenti, come l’insieme delle combinazioni lineari a coefficienti interi dei vettori della base. Gli schemi selezionati dal processo di standardizzazione del NIST, sia KEM che firme, appartenenti alla lattice-based cryptography sono costruiti a partire dal problema del Learning With Errors (LWE) [6]. Dato un sistema di equazioni lineari random che descrivono un segreto, il LWE si basa sull’idea di nascondere il valore del segreto aggiungendo del rumore al sistema. Nel corso degli anni sono state proposte delle varianti strutturate del LWE allo scopo di diminuire la dimensione della chiave pubblica: Ring-LWE e Module-LWE.

Codici
Altri oggetti matematici di importanza rilevante nella PQC sono i codici (o codici a correzione d’errore). Questi nascono nel contesto delle telecomunicazioni per individuare e correggere errori che possono verificarsi nella trasmissione attraverso un canale rumoroso e sono stati introdotti nel contesto della crittografia con lo schema di Robert McEliece [7] nel 1978. A partire da questo sono stati progettati altri algoritmi PQC, sia KEM che firme, costruiti su problemi riconducibili al più generale Decoding Problem, ovvero il problema della decodifica di un vettore contenente un errore.

Hash
Le funzioni di hash hanno un ruolo fondamentale in numerose costruzioni crittografiche. In particolare, nel panorama PQC le funzioni di hash possono costituire l’elemento cardine di una firma. È interessante notare che nelle firme hash-based la sicurezza non si basa su un problema matematico, bensì sulla proprietà di generiche funzioni di hash.

Maturità percepita

Tra le firme, quelle hash-based vantano il fatto che risulterebbero attaccabili solo se fosse possibile compromettere la funzione di hash utilizzata al loro interno. In quanto componenti comuni ad altre firme, una vulnerabilità di questo tipo avrebbe ripercussioni così estese da non essere ritenute plausibili. Questa è percepita dalla comunità scientifica come una garanzia di sicurezza. A sostegno della sicurezza della lattice-based cryptography, sebbene sia più recente (il primo schema è del 1996 e il LWE del 2005), vi è un peculiare risultato teorico [8] che ne ha rafforzato la fiducia e ha in parte favorito la predominanza di schemi basati sui reticoli nel processo di standardizzazione NIST: alla fine del terzo round sono stati scelti CRYSTALS-Kyber [9] per la negoziazione chiave e CRYSTALS-Dilithium [10], Falcon [11] e SPHINCS+ [12] per le firme digitali post-quantum. Tutti, tranne SPHINCS+ che è hash-based, sono costruiti sui reticoli. Rimane fuori dalle scelte del NIST, per ora, la code-based cryptography con lo schema più conservativo: Classic McEliece [13]. Nel tempo, questo schema ha resistito a numerosi tentativi di crittoanalisi e ha dimostrato un’elevata affidabilità ed efficienza in termini di prestazioni. Nonostante ciò, il principale svantaggio, che negli anni ha ricevuto soluzioni solo parziali o insicure, è quello della dimensione delle chiavi pubbliche che rende questo schema di difficile utilizzo in contesti con stringenti requisiti di memoria o banda.

Transizione al post-quantum

La transizione verso nuovi standard crittografici comporta storicamente numerose sfide. Nella migrazione ad algoritmi post-quantum, si possono identificare processi separati per gli schemi di scambio chiave e di firma digitale. Un caso di studio particolarmente interessante per le sue applicazioni è il TLS [14]. Nel protocollo TLS, sebbene la sicurezza di una comunicazione attiva sia garantita da algoritmi simmetrici, non impattati dall’avvento del quantum computer, l’avvio del protocollo richiede un metodo per scambiare la chiave (simmetrica) crittografica ed è necessario verificare l’identità del server a cui si è connessi (e talvolta anche quella del client). In questa fase, detta di handshake, entrano in gioco algoritmi asimmetrici di negoziazione chiave, per garantire confidenzialità della comunicazione, e di firma digitale, per l’autenticità. Entrambe sono proprietà irrinunciabili in un protocollo di comunicazione sicura come il TLS, ma la sostituzione degli algoritmi sottostanti presenta sfide e orizzonti temporali differenti. Ad oggi, l’algoritmo maggiormente utilizzato nella fase di negoziazione chiave del TLS è lo schema ECDH X25519 [15]. L’alternativa post-quantum in fase di standardizzazione è lo schema ML-KEM (Kyber), uno schema KEM basato su reticoli. DH e KEM sono due diversi paradigmi di negoziazione chiave, il primo di difficile realizzazione in ambito post-quantum. Sebbene presentino potenziali incompatibilità dovute alla necessaria interattività dei KEM (Fig.2), l’utilizzo di un KEM nel TLS non presenta difficoltà.

Figura 2: DH vs KEM. I KEM richiedono sempre un round di interazione dopo lo scambio delle chiavi pubbliche

Clicca qui per ingrandire l'immagine

D’altra parte, ML-KEM ha dimensioni molto maggiori, anche nella versione ML-KEM-512 che corrisponde allo stesso livello di sicurezza di X25519 (Fig.3).

Figura 3: Confronto tra ECDH X25519 e KEM PQC Kyber, nelle sue tre versioni di sicurezza

Clicca qui per ingrandire l'immagine

Sperimentazioni guidate da Google [16] e Cloudflare [17] hanno dimostrato come l’incremento di dimensioni introduca un aumento di latenza trascurabile nell’handshake TLS. Le nuove dimensioni possono però indurre una frammentazione dei pacchetti di handshake, causando possibili incompatibilità con dispositivi legacy. La migrazione di questi apparati rappresenta una delle principali sfide nell’introduzione di KEM PQC. Le firme PQ, contrariamente ai KEM, non presentano differenze funzionali rispetto agli schemi tradizionali. Ciò nonostante, lo stato di queste primitive appare oggi più complesso. Il NIST sta definendo gli standard di tre schemi: ML-DSA (Dilithium), FN-DSA (Falcon) e SLH-DSA (SPHINCS+). La difficoltà nel sostituire gli algoritmi classici risiede nell’uso eterogeneo che viene fatto di questa primitiva. Nel TLS, ad esempio, le firme hanno ruoli e requisiti diversi a seconda che vengano utilizzate durante l’handshake o nella verifica dei certificati. Nessuno degli schemi PQ attualmente proposti risulta particolarmente indicato per tutti i ruoli, d’altra parte utilizzare schemi multipli aumenta gli sforzi implementativi e la superficie di attacco. Ad oggi, solo la versione più compatta di ML-DSA (Dilithium-2) ha una combinazione di dimensioni e prestazioni compatibili con i tradizionali Ed25519 e RSA (Fig.4); essa, tuttavia, introduce 17 KB di overhead rispetto agli algoritmi tradizionali, con conseguenze più marcate rispetto all’uso dei KEM PQC. Lo stato parzialmente insoddisfacente delle firme digitali ha portato il NIST ad avviare nel 2023 un ulteriore processo dedicato [18].

Figura 4: Confronto tra firme digitali tradizionali e PQ

Clicca qui per ingrandire l'immagine

Protocolli ibridi
Per facilitare la migrazione e ridurre l’impatto di possibili vulnerabilità negli algoritmi PQC, è possibile combinare la crittografia tradizionale e quella PQ tramite un approccio ibrido (Fig.5) nel quale la componente PQC difende da un attacco quantistico, mentre quella classica da una vulnerabilità dell’algoritmo PQC. Tale approccio rappresenta un passaggio intermedio importante nella transizione completa alla PQC, poiché di facile realizzazione e con immediati benefici di sicurezza.

Figura 5: Negoziazione chiave ibrida tramite combinazione DH e KEM PQC

Clicca qui per ingrandire l'immagine

Conclusioni

Il processo di standardizzazione delle tecnologie post-quantum si trova nelle fasi conclusive e l’industria si sta preparando alla transizione. Nel contesto delle comunicazioni web, l’integrazione di algoritmi PQC nel protocollo TLS garantirà già nel breve termine la confidenzialità dei dati rispetto ad avversari quantistici. Oltre al TLS, la migrazione alla PQC riguarda numerosi altri protocolli che impiegano la crittografia a chiave pubblica. Alcuni, come SSH o i protocolli VPN come IPSec e WireGuard, condividono le caratteristiche e le sfide evidenziate per il TLS. Altri, come DNSSEC o protocolli basati su primitive più avanzate, non presentano ad oggi alternative PQ praticabili e rappresentano interessanti direzioni di ricerca.
Nonostante i processi ancora in corso, l’industria ha oggi gli strumenti per avviare la transizione a tecnologie post-quantum, valutandone l’impatto sui processi e selezionando gli algoritmi migliori per i casi d’uso specifici. Una preparazione attenta è oggi fondamentale per mitigare la minaccia del QC, così da garantire la sicurezza delle informazioni a lungo termine.

Riferimenti

Feynman, R.P.: Simulating physics with computers. Int J Theor Phys. 21, 467–488 (1982). https://doi.org/10.1007/BF02650179
GSM Association: Post Quantum Telco Network Impact Assessment. GSM Association (2023)
Agence Nationale de la Sécurité des Système d’Information (ANSSI): ANSSI views on the Post-Quantum Cryptography transition (2023 follow up). ANSSI (2023)
Bundesamt für Sicherheit in der Informationstechnik (BSI): Cryptographic Mechanisms: Recommendations and Key Lengths. BSI (2024)
NSA Releases Future Quantum-Resistant (QR) Algorithm Requirements for National Security Sy, https://www.nsa.gov/Press-Room/News-Highlights/Article/Article/3148990/nsa-releases-future-quantum-resistant-qr-algorithm-requirements-for-national-se/http%3A%2F%2Fwww.nsa.gov%2FPress-Room%2FPress-Releases-Statements%2FPress-Release-View%2FArticle%2F3148990%2Fnsa-releases-future-quantum-resistant-qr-algorithm-requirements-for-national-se%2F
Regev, O.: On Lattices, Learning with Errors, Random Linear Codes, and Cryptography. JACM. 56, 84–93 (2005)
McEliece, R.J.: A Public-Key Cryptosystem based on Algebraic Coding Theory. DSN Progress Report. 44, 114–116 (1978)
Ajtai, M.: Generating hard instances of lattice problems. In: Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. pp. 99–108 (1996)
Schwabe, P., Avanzi, R., Bos, J., Ducas, L., Kiltz, E., Lepoint, T., Lyubashevsky, V., Schanck, J.M., Seiler, G., Stehlé, D., Ding, J.: CRYSTALS-KYBER. National Institute of Standards and Technology (2022)
Lyubashevsky, V., Ducas, L., Kiltz, E., Lepoint, T., Schwabe, P. r, Seiler, G., Stehlé, D., Bai, S.: CRYSTALS-DILITHIUM. National Institute of Standards and Technology (2022)
Prest, T., Fouque, P.-A., Hoffstein, J., Kirchner, P., Lyubashevsky, V., Pornin, T., Ricosset, T., Seiler, G., Whyte, W., Zhang, Z.: FALCON. National Institute of Standards and Technology (2022)
Hülsing, A., Bernstein, D.J., Dobraunig, C., Eichlseder, M., Fluhrer, S., Gazdag, S.-L., Kampanakis, P., Kölbl, S., Lange, T., Lauridsen, M.M., Mendel, F., Niederhagen, R., Rechberger, C., Rijneveld, J., Schwabe, P., Aumasson, J.-P., Westerbaan, B., Beullens, W.: SPHINCS+. National Institute of Standards and Technology (2022)
Albrecht, M.R., Bernstein, D.J., Chou, T., Cid, C., Gilcher, J., Lange, T., Maram, V., von Maurich, I., Misoczki, R., Niederhagen, R., Paterson, K.G., Persichetti, E., Peters, C., Schwabe, P., Sendrier, N., Szefer, J., Tjhai, C.J., Tomlinson, M., Wang, W.: Classic McEliece. National Institute of Standards and Technology (2022)
Rescorla, E.: The transport layer security (TLS) protocol version 1.3. RFC Editor (2018)
Langley, A., Hamburg, M., Turner, S.: Elliptic Curves for Security. RFC Editor (2016)
Experimenting with Post-Quantum Cryptography, https://security.googleblog.com/2016/07/experimenting-with-post-quantum.html
The TLS Post-Quantum Experiment, https://blog.cloudflare.com/the-tls-post-quantum-experiment
Computer Security Division, I.T.L.: Call for Proposals - Post-Quantum Cryptography: Digital Signature Schemes | CSRC | CSRC, https://csrc.nist.gov/projects/pqc-dig-sig/standardization/call-for-proposals

Acronimi

ANSSI Agence Nationale de la Sécurité des Système d’Information (National Cybersecurity Agency of France)

BSI Bundesamt für Sicherheit in der Informationstechnik (Federal Office of Information Security)

CNSA Commercial National Security Algorithm Suite

DH Diffie-Hellman

DSA Digital Signature Algorithm

ECDH Elliptic Curve Diffie Hellman

KEM Key Encapsulation Mechanism

LWE Learning With Errors

NIST National Institute of Standards and Technology

NSA National Security Agency

PQC Post Quantum Cryptography

QC Quantum Computer

SSH Secure Shell

TLS Transport Layer Security

VPN Virtual Private Network